Swiss Tables Design Notes
Abseil provides its own family of hash tables (colloquially known as “Swiss
tables”) in place of std::unordered_set and std::unordered_map. These
classes are:
absl::flat_hash_mapabsl::flat_hash_setabsl::node_hash_mapabsl::node_hash_set
This design note explains how these tables were implemented, the performance
improvements our tables provide in certain cases, and why those might make you
choose them over std::unordered_{set,map}.
Lookup Optimizations
Swiss tables hold a densely packed array of metadata, containing presence information for entries in the table. This presence information allows us to optimize both lookup and insertion operations. This metadata adds one byte of overhead for every entry in the table.
Metadata Layout
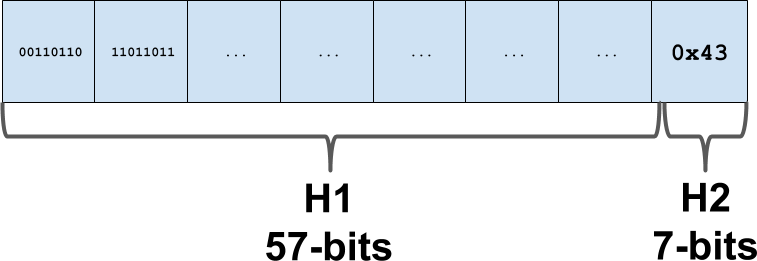
Within Swiss tables, the result of the hash function produces a 64-bit hash value. We split this value up into two parts:
- H1, a 57 bit hash value, used to identify the element index within the table itself, which is truncated and modulated as any normal hash value would be for lookup and insertion purposes.
- H2, the remaining 7 bits of the hash value, used to store metadata for this element. The H2 hash bits are stored separately within the metadata section of the table.
For performance reasons, it is important that you use a hash function that distributes entropy across the entire bit space well (producing an avalanche effect). The Abseil hash framework accomplishes this well and should be sufficient for most users.
Metadata Information
The metadata of a Swiss table stores presence information (whether the element is empty, deleted, or full). Each metadata entry consists of one byte, which consists of a single control bit and the 7 bit H2 hash. The control bit, in combination with the value in the H2 section of the metadata, indicates whether the associated hash element is empty, present, or has been deleted.

The metadata, which is an implementation detail but can be thought of as being laid out consecutively, maps this presence information to elements in the hash table itself.

In this diagram, elements with the same H1 hash are colored identically, blue elements are empty, and black represents a deleted element.
Metadata Lookup
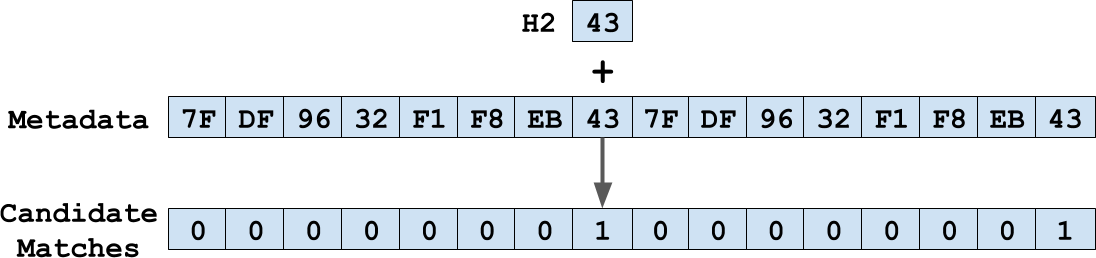
When searching for items in the table we use SSE instructions to scan for candidate matches. The process of finding an element can be roughly summarized as follows:
- Use the H1 hash to find the start of the “bucket chain” for that hash.
- Use the H2 hash to construct a mask.
- Use SSE instructions and the mask to produce a set of candidate matches.
- Perform an equality check on each candidate.
- If no element is found amongst the current candidates, perform probing to generate a new set of candidates. Note that a deleted element does not cease probing, though an empty element would.
Steps 2+3 can be summarized visually as:
Equivalent code for this lookup appears below:
Mask Match(h2_t hash) const {
auto match = _mm_set1_epi8(hash);
return Mask(_mm_movemask_epi8(_mm_cmpeq_epi8(match, metadata)));
}
This process is an important performance trick. Because we can winnow 16 candidates down to only those with a matching H2 hash in only a few instructions, we are functionally searching very deep probe chains inexpensively.
Storage Optimizations
In addition to optimizations made in relation to element insertion and lookup,
Swiss tables were designed to also optimize certain operations that were
especially non-performant on std::unordered_map.
Allocation Optimizations
In STL containers, emplace() will almost always:
- Allocate a value_type on the heap.
- Try to insert the allocated entry.
- If the insert fails, delete the allocated entry.
We avoid this allocation in all cases where the key can be inferred from the
arguments of emplace() without running user-defined constructors.
absl::flat_hash_map<int64, std::string> m = {{0, ""}};
// No objects of type `std::string` are constructed in the following code.
m.emplace(0, "abc");
m.emplace(std::make_pair(0, "abc"));
m.emplace(std::piecewise_construct,
std::forward_as_tuple(0),
std::forward_as_tuple("abc"));
The same optimization is applied for insert() operations.
Move Optimizations
Similarly, we separate a hash element’s value_type (the type of an entry) from
its init_type (the type from which an entry can be constructed) to allow
insertions to consume arguments. This allows initializers to std::move() on
construction instead of requiring a copy.
// No strings are copy-constructed in this example.
// std::unordered_map would have performed one string copy.
absl::flat_hash_map<string, int> m;
m.insert({"hello", 42});
As well, for both copy and move operations, try_emplace(), if the insertion
does not occur because the key already exists, will neither copy nor move
(respectively) the original elements.
Credits
NOTE: The design and implementation of Swiss tables involved many people, but in particular, we’d like to acknowledge the major contributions (in alphabetical order) of Sam Benzaquen, Alkis Evlogimenos, Matt Kulukundis, and Roman Perepelitsa.